Verics supports two basic types of input formats for specifying models: a low-level
a high-level. The low-level Vxs format, seen elsewhere in the tutorial, has a 1:1
mapping to a Markov process and is mainly intended for small- to moderate-
models with a strict definition to the level of individual states and transitions.
The high level formats allows a more programmer-friendly specification of a model,
by using familiar concepts like classes or for loops. A number of optimisations
is performed when translating a high-level model, they produce a logical counterpart yet the user
can not completely control each detail of the respective output automaton, as it is with a
typical optimising compiler of a high-level language. There are two high
level formats currently supported: an instrumented subset of the Java language and the
Verics language. These are mostly interchangeable, although the Verics language is more
focused on modelling.
The Verics language can also be used as a preprocessor in the Vxs files. You will find some snippets of Verics in several examples of low-level automata in this tutorial.
Let us discuss a translation and then checking of an example Java model: a probabilistic game which models a distributed energy management system, as presented in [1]. We will start with a description of choices, ranges, clocks and games (or agent systems) before describing the model.
1. Threads
Operations within a model specification can be executed by either a single
Like in a regular Java application, the two types of threads may share code, by e.g. calling the same methods. Yet, there are operations that only one of the thread types supports. The divide is mostly intuitive – for example, the main thread is not able to synchronise with other threads, as when it is alive, it is all alone, the automaton threads exists as definitions only. An automaton thread, in turn, can not create arbitrary objects, in order to fit into some rigid automaton formalism enforced by model checkers.
Note that the main thread is executed by Verics's internal interpreter, and so it is not very fast. It is typically speedy enough to create complex topologies of automatons, but might be way too slow for performing intensive computations.
After the main thread ends (or in certain models almost ends, we will return to that later), Verics begins to analyse the state of the translated application, including searching for all running automaton threads, which, even that started, did not perform a single operation yet. They will do so, in a sense, only in simulators or in analytic engines of model checkers.
2. Choices
There is a support for conditional, probabilistic and (if Markov processes are allowed) non-deterministic choices, defined through different statements.
2.1. Conditional
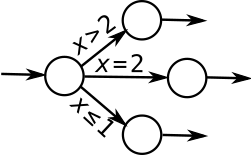
A conditional choice is a state with
a number of transitions such that they have complementary guards, i.e.
always one and only one is true. Such an automaton can be a result of
a translation of one or more constructs
like Java's if, where the condition is an expression that
can be reduced to boolean comparisons of a mix of variables and constants.
As a volatile variable (understood as one that can be modified by several threads), if evaluated multiple times, might yield a set of different values, a care is taken, that testing of such variables in the output automaton matches exactly the one in the source code. For non--volatile variables, though, optimisations can be applied, which collapse several evaluations into a single one. Here is an example of such a collapse:
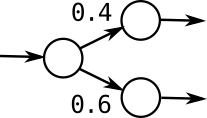
2.2. Probabilistic
A probabilistic choice is translated from conditional expressions
that are of the form if(Math.random() < i).
A choice of that type is translated into a state with two transitions,
each decorated with a probability value, and these two values sum to 1.
For example, the mentioned construct would be translated as seen below:
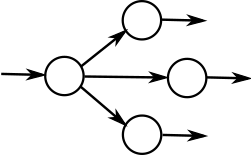
A probabilistic choice defined using a single if has only two outgoing transitions.
To overcome that limitation, there is also available a balanced
n--ary probabilistic choice, that is translated into n
transitions outcoming from a single state, each labelled with a probability 1/n. It is defined
using an expression (int)(Math.random()*n), which is
typically assigned to a variable.
2.3. Nondeterministic
A nondeterministic choice allows Markov decision processes, i.e. a superset of Markov chains. A nondeterministic choice specifies no rules of choossing its branches. This models a lack of knowledge about the model. The rules can be found by e.g. a model checker which searches for an optimal strategy.
A nondeterministic choice is modelled in Java by a construct Random.nextInt(b), where b specifies a number of nondeterministic outcomes. The value returned by the function can be tested in different ways, in order to split a path nondeterministically.
See that a nondeterministic choice implemented as above is in fact a probabilistic choice within a JVM. This is because nondeterminism in general can not be implemented in a runtime, as it models an unknown behaviour (possibly, nondeterministic, deterministic, probabilistic or any mixture of these).
3. Ranges
An allowable range of values of a variable or a primary expression can be defined within a comment. Thanks to this, the model can still be a valid Java program. A range contains two expressions, representing respectively a minimum and a maximum allowed value. Such an expression can refer to any variable in a given scope, butVerics must
be able do evaluate the expression into a constant value, after the main
thread ceases to modify the application. For that end, the compiler performs
a number of optimisations in order to replace expressions with constants.
Ranges on variables are roughly translated into ranges on state variables in the output
file. Yet, if Verics can not verify by itself, that a given limit won't be violated,
it widens a state variable's range, so that it can also generate an accompanying PCTL property
to check for any violations of that limit. Ranges on expressions, due to their locality, are translated
into sub-automatons. An invalid value leads though these into an error state.
4. Clocks
For a better support of timed automatons [2], Verics has a number of clocks operations. Let v be time in seconds. BesideThread.sleep(1· 103 v),
that was effectively translated to two serial transitions: x := 0,
x >= v (x is a clock variable), there are also methods Sleep.exact(v),
Sleep.min(v) and Sleep.max(v) that put
different relational operators on the second transition.
4.1. Probabilistic
Depending on the probability distribution of delay times, these methods can have a parameter having one the following forms:
- a constant distribution, x = v :
Sleep.*(v); - a probabilistic negative exponential distribution,
x ∊ (0, ∞):
Sleep.*(Dist.nxp(λ)); - a probabilistic tabularised distribution x ∊ (v1, vN):
Sleep.*(Dist.tab(v, ρ)); - a non--determined, unknown distribution, x = 0, 1, . . . v - 1:
Sleep.*(Random.nextInt(v)).
Not all of these constructs are supported in all backends.
4.2. Schedulers
Wherever there is no clock condition or invariant on a state or on a transition, by default any duration time is assumed. That can be modified by5. Games
A Java thread, or effectively an automaton, can be declared as a player. These players can form coalitions. Prism's rPATL properties can then be used to find out e.g. optimal strategies of coalitions.
As Prism accepts only turn–based games, only a single player can move at once,
and that quality must be explicitly seen by Prism. It would be impossible to implement such a game by using Java's locks,
as, due to the way Verics works, there are always at least two automatons involved in a
wait()/notify() operation,
one of these is a special lock automaton. Thus, a different synchronising mechanism
is used in turn–based games – a conditional barrier. It is directly translated
into synchronising labels, and optional conditions on leaving a barrier
are translated to guards of these labels.
For easier implementation of a game, a small Java library for implementing games is included with Verics. It employs player synchronisation in a way compatible with the requirements of Prism.
Using the
6. Case study
Let us analyse an example model of a distributed energy management system [1]. There is a related case study on the Prism site for a more detailed description of the model and also an implementation in the Prism language.
Incidentally, we will also discuss some detailed features of Verics not mentioned earlier in this tutorial, if applicable.
The said model consists of a local source of electrical power that forms a microgrid together with a number of nearby households. Similar schemes are becoming popular on energy markets, where small power providers, like wind turbines, perform a complementary service to the global grid. The algorithm, if followed by the receivers of energy, smooths out peaks in demand.
There is a scheduler (a distribution manager) and N households. At the beginning of each time interval (there are 16 of them per day), the scheduler chooses one of the households at random and then proposes it to buy a load (consume a quantity of electric energy) at a given price. The price, within a single time step, is equal to the total number of loads consumed currently by all households, including the additional load to be bought.
The probability, that a household needs to buy a load, is determined by a daily demand curve. The duration of the load is random, between 1 and few time intervals. A household does not react to any possible further buy inquiries while it is consuming the load. If a household wants to buy a new load, it is obliged to choose the microgrid if the price is below a given threshold clim. Otherwise, a household must perform a drawing, which with a constant probability Pstart decides, that the load must be bought from the microgrid. If this is not the case, that is, with a probability 1 - Pstart, the household is granted the right to back–off, e.g. by choosing a global grid instead. It is unknown, in which way a household will take advantage of that right.
The system can be modelled as a game, here with N + 1 agents or players: the scheduler and each of the households. As a household has a choice of unknown characteristics, then it is non–deterministic – it thus has a strategy which is not specified in the model.
6.1. Source file
The model is a
The beginning of our model specification, that provides all of the necessary imports, is as follows:
Let us follow the rules of modular programming and divide the model into N + 2 entities – the microgrid itself, a scheduler, and N households. And so, we begin with the microgrid:
Microgrid.
This is the only public class in the source file, and thus the class gives its name
to the file.
Also, the Microgrid class contains the main method, which sets up the whole model.
The microgrid has a number of basic traits, that must be defined, like the number of households, or the demand curve. Let us define these:
Microgrid, part 1.Also, a few variables are needed to store the state of the system:
Microgrid, part 2.The microgrid must know, who its users are (line 4). It also remembers the current time in intervals (line 8), and can store the total number of loads being executed (line 12).
There are
The compiler
can analyse subexpressions with ranged operands, in order to estimate the range
of the whole expression's result. Thus, sometimes even a few scattered ranges may
help Verics iteratively determine the missing ranges. If not found, a default
range is assumed, which, for the type int, is 〈-215 + 1, 215 - 2〉.
Let us see, what the main thread does, in order to create the microgrid. The main thread always starts with the main method:
Microgrid.
In line 4, a helper object from a game package from Verics's library is created. Thanks to
using that package,
some boilerplate code will be avoided in the model. In the next line, one of the
methods of the Model class is called. The class gives some control over the output
file generated by Verics. In this particular case, it is specified that any
field variables belonging to table should not be decorated with any prefixes
or suffixes in the output files, raw names only. The method Model.name(Object, String prefix, String suffix),
and the convenience methods Model.name(Object, String suffix),
Model.name(Object) make names of state variables in the
output file shorter and predictable by adding a prefix and a suffix to the field name.
If such a custom naming scheme is used, though, then the user must arrange the naming so that there
are no resulting name conflicts. Object in the methods discussed can also be an array reference,
in such a case concatenated prefix and suffix alone refer to the referenced array (not to the
field).
Local variables, as opposed to non-static fields, do not fall into the naming scheme, and thus have the default, conflict–free yet verbose and unpredictable names. This is usually not a problem as locals are assumed to be generally not used within the properties checked anyway, also because of the way an optimiser may treat a local (e.g. replace it with a constant, specific for some method call). Designate a field if you want to test its values.
The loop in lines 8–14 creates households. The class Household is a thread,
and thus its creation and starting causes an automaton to be generated. In the loop,
there is a yet not discussed method Model.player(), that makes
an automaton thread a named participant in the game.
There is a number of households, so we append numbers to their field names – otherwise Verics would complain about duplicates. There is only a single scheduler, so raw field names are enough in its case.
In line 21, a field, and in effect a state variable, time, is initialised. In Java,
integer fields are initialised with 0 anyway, so the instruction is not needed in fact,
but serves as an example of a fragment of the definition of an initial state.
The next operation uses the helper table object to start the game. There are
N + 1 players declared – Verics will check, if it is a correct value.
The value is in fact the number of objects, that use a conditional barrier,
which synchronises players – but in the case of a TurnGame the value is
the same as the number of players.
The statement is the first one executed by the main thread,
that would actually made the automaton threads active (in the sense of `not only waiting on a barrier')
if on a JVM. This is why the initial state could still be specified (line 21)
despite that the automaton threads had already been started using Thread.start(). Because
of the discussed assumption within Verics, that automaton threads never become active before the
main thread ceases to be active, a situation where both types of threads
The next thing to do in the main thread is to specify the properties to check. These will be put into a respective file, unless Verics works in the range–checking mode, in which special range–checking properties are generated instead. As can be seen, Verics's interpreter may be a help in generating long sequences of PCTL or rPATL properties.
The statement Model.waitFinish() in line 29 waits until some automaton thread
encounters an operation Model.finish(). This may seem contradictory to the
way Verics works – as has been said, the compiler exits without interpreting any
automaton thread. So, it would need to wait forever in Model.waitFinish().
Instead, Verics's interpreter treats the statement as a signal to immediately
finish interpreting of the main thread – any statement in lines 30–34 is
invisible to Verics. These are only of use if the model is run on a JVM – you may
thus specify code, that runs once the automaton threads declare, that the simulation
ends – yet note, that consequently Model.finish() can only be executed
if the automaton threads will no longer modify any variable.
In our case, we use Model.waitFinish() to wait until the final simulation
time is displayed. Then, we would like to terminate all automaton threads, in order
to cleanly end a process. The
scheduler ends by itself, but households wait on the barrier. They can be terminated
at once by taking advantage of that barrier's property, which says, that if any
thread waiting on it is interrupted, then all of these threads enter the
interrupted state, as specified in the Java standard, and then leave the barrier.
The statement at line 35 starts just that process.
A counterpart statement in the definition of a household checks, if
the household's automaton thread is in an interrupted state, and if yes, then
leaves the loop immediately (Listing 14, lines 5–6).
Because Microgrid declares a number of fields that characterise the microgrid in general,
let us also put some specifically
microgrid–related functions into the class as well. All of the methods, as opposed
to the main one, will in our case be only called by the automaton threads.
Let these methods be static.
What is static and what is not is often the matter
of programming style, not to be discussed here. Let us just mention, that
these methods belong to a class and to its instance because they are utility methods of Microgrid, which does not itself have any instances –
there is only a single microgrid created. Were there more grids in a single network
of automatons, we would make an instance of appropriately rewritten Microgrid for each,
and getNumJobs() would not be static anymore. Were there separate demand curves
for each microgrid, the array DEMAND would not be static, and in effect,
getDemand() were an object method as well.
Let us now look at the contents of several methods, that report the microgrid's state.
Microgrid, part 1.
See that the method getDemand() not only uses an array, but also returns a
variable floating–point value. Both arrays and non–integer variables
are not supported in some model checkers, e.g. in Prism.
Yet, Verics has a number of translation techniques, like streamlining
the code or emulating arrays, that attempt to remove or replace unsupported elements. The compiler
does not always manage, though, to optimise out all double variables, partly because
there are e.g. strict rules on the order of accessing fields so to not inadvertently
modify a model's behaviour.
The next method, getNumJobs(), returns how many households generate a load at
the current time. There is a range definition on the local numJobs –
obviously, the number of jobs can never be larger than the number of households.
We could also put the same range on the return value of the method, yet that would not change a
thing – Verics finds out by itself, that getNumJobs()'s range results
from the one of numJobs. Yet putting the range numJobs – Verics does not know, if numJobs
is allowed to be outside 〈0, N〉, before flow of control reaches the return
statement.
In the next listing, we have two methods related to the end of a single time interval. The comment of the first method describes it precisely. The method will be used by the scheduler to decide, if to end its activity.
Microgrid, part 2.
The second method, endInterval(), does several things needed at the end of each
time interval. Firstly, it puts the number of jobs
i.e. loads of electricity, into a field. It does so only to measure that value
by a model checker – this is why Model.state() saves a position within an automaton
after the field (a fragment of the state vector) already has the current value, assigning a label to reference that position.
Another purpose of the method endInterval() is to decrease by one the counters,
that represents lengths of time that are left each load.
Let us browse the thread classes of each player, beginning with the scheduler.
Scheduler.
Scheduler is a subclass of TurnPlayer, which is provided by the game
package, and which itself is a subclass of Thread.
Scheduler.
The scheduler (not to be confused with Verics' schedulers)
is normally probabilistic, but it also has a modifier, that can make it non–deterministic
instead – if NON_DETERMINISTIC is true, a strategy is decided by a Random object.
Random is the simplest case of declaring strategy. Special wrappers for writing custom
choice methods, or for declaring a common strategy, exist in Verics's library.
The scheduler has also a constructor, called by the main thread:
Scheduler.
The statement in line 2 passes to the super-class TurnPlayer a reference to the game in which
a player participates, and also the player's number. The number is required by the logic
rPATL. Here, the scheduler is assigned 0. The households declare in their constructors
subsequent numbers 1, 2, . . . N.
There is yet another method in Scheduler – run(), which is a top method
of a thread, and thus also a top `method' of the respective automaton:
Scheduler.
The constant NON_DETERMINISTIC is set within the main thread, so at the time of generating
this automaton, it is exactly known which branch of the choice in lines 6–13 is unconditionally executed,
and which branch is dead. The compiler takes use of that knowledge and removes completely
the condition at line 6 and one of the branches from the automaton.
There is a probabilistic choice in lines 12–13. As discussed,
the exact behaviour of that kind of choice, as opposed to the non–deterministic one,
is known – in this
case, draw a natural number in the range 0, 1, . . . N - 1, using an uniform probability
distribution. Thus, if NON_DETERMINISTIC is false, the scheduler, even that it is a player,
has only a single, hard–wired strategy, defined in the very model.
After a household is selected by the scheduler by setting the local variable address, that
exact household has a next move.
The next player to move is declared by the player that currently moves,
using a super-class' method turnNext(i), where i is the player's number (line 15). After
the scheduler selects the next player to move, it
waits for its own move using turnWait() (line 16). When a time of its move comes again, the discussed
Microgrid.endInterval() is called.
The scheduler's loop condition in line 19 calls a method Microgrid.isFinished(), which
returns, if to end the simulation. If yes, then the already mentioned method Model.finish() is
called and the scheduler ends. For a model checker it means, that the scheduler's
automaton will stay in some final state forever. For a JVM it means, that the scheduler's
thread will return from the method run(), and thus will terminate.
The class of a household should now be self–explaining.
A number of constants, directly related to a household, is declared here, and not in Microgrid:
Household.
In particular, the constant clim is represented by PRICE_LIMIT, and
similarly, Pstart is implemented as P_OVER_LIMIT.
There is also job variable. If zero, the household does not generate a load. If non–zero,
then the field expresses the time left of generating the load bought, in intervals.
A household has a constructor, executed by the main thread, like it was in the case of Scheduler:
Household.
and, as TurnGame is a thread, the run() method:
Household.In lines 5–6, the already discussed loop exit statements are seen. They have no effect on an automaton generated by Verics, as neither Verics's interpreter, nor automatons themselves, can cause an interrupt. The sole reason of these statements is to take part in stopping a Java application on the JVM side.
In line 7, there is another variant of a probabilistic choice –
Math.random() < Microgrid.getDemand()*EXPECTED_JOBS. This time
a boolean condition is evaluated, by comparing a random value, drawn using an uniform distribution,
to a variable value, that here translates to a probability of this if's sub-condition becoming true.
There is yet a third, rather self–explaining method in Household, called by Microgrid.endInterval()
(the call statement is located in Listing 7, line 19) on each household whenever a
time interval ends.
Household.
The source code we studied is enough to generate a model. In fact, it also generates a series of
properties in a probabilistic logic.
But model checkers may have also other features, not explicitly supported by Verics. A
Here, reward structures for Prism are seen. The term measure refers to a formula generated by
Verics, thanks to the statement in line 15 of Listing 7. We will
return to that formula later.
So, let us generate Prism–compliant files, but before, there is the question which Scheduler).
Schedulers, as mentioned, define time invariants on states, but in effect also, what kind of order of operation is
possible within a network
of automatons. There is the default scheduler that leaves an automaton as is – with that scheduler applied,
any state, by default, e.g. without delay operations like Thread.sleep(),
may last any time from 0 to infinite, unless some
Let us run Verics:
$ hc -sh -i -op -v0 Microgrid.java
In the case of a Prism model, there are two files generated:
Microgrig.nm contains a model of a Prism's type smg, because players were defined,
and Microgrig.pctl contains the properties to check.
The output model file will contain formulas that represent states saved with Model.state(), and also
all final static fields, extracted from the model. These can be, thus, used in properties
or in the appended verbatim section.
The formula measure is added thanks to the call at line 15 in Listing 7.
As turnEnd() is called by the scheduler, the formula points to the local variable
of the automaton Scheduler.
Naming conventions are not applied to the constants, even that they are fields, as these fields are
static, an thus are not owned by any object passed to Model.name(). Instead, a field's name
is directly used, and in the case of a name conflict, the name is prefixed with that
of a respective class.
In the case of an output for Prism, the compiler generates yet another file, a one with properties, whose initial fragment is as follows:
As seen, the expressions make use of player numbers declared in constructors of automaton threads,
of a reward structure appended to the model as seen in Listing 16,
and of a state variable time, declared in Listing 4.
A property that checks for a total expected value of a household after the simulation
ends might contain time=MAX_TIME.
6.2. Range checking
Let us shorten the array with the demand curve by one element, so that its new size is 15, and thus not as much as the number of time intervals per day.
The array is indexed with time % INTERVALS, as seen in line 5 of
Listing 6. The variable time can be as large as
MAX_TIME = 48, and that maximum value (amongst some other values), modulo
INTERVALS, is greater than the new array size. Clearly, indexing of
DEMAND would be incorrect for certain time intervals.
The compiler, though, is not able to prove in this case, if
time
Let us include, for completeness, the formula generated to emulate indexing of the array:
Note that the expression time % INTERVALS is embedded within the formula. It is an example
of Verics's attempts at simplifying the vector state when generating to Prism.
6.3. Locals and fields
The compiler does not treat local variables very seriously,
as it assumes, that only the field variables are generally checked. Yet, it does not mean
that locals are always optimised out. For example, the source model might
store the contents of a field in a local, and then the local might be read multiple
times. Verics could get rid of the local and make the generated automaton read the field
multiple times instead. Yet, the compiler is careful in such situations – it does not know,
if the field is modified by another automaton in the meantime. Verics would
not even join field accesses from two serial transitions into a single transition,
as the merged transitions would mean
The compiler can be much more lax in the case of locals. See the update in the following listing.
The long name indicates a local variable. The name contains an instance of an object, and
also a trace of subsequent method calls.
See that the variable is read, and then immediately
As field variables are never reset by Verics, it is sometimes advantageous to do that by hand. See Listing 7, line 16, for an example of a source–level reset.
6.4. Analytic vs statistical
Models that work best with Prism's analytic engines may differ from these that work better
with simulators. This is why hc provides a method Model.isStatistical() in
its library. The method's
default return value is false within Verics, but true within a JVM. You may
use that function in the model's source to tune that model to the way its properties will
be computed by a model checker.
Let's modify Microgrid.java to adapt to Model.isStatistical().
In the case of Prism, it can be more important to reduce the number of states. In the cases
of JVM or of a simulator, reducing the number of operations may matter more.
The original model aimed at the former – this is why Microgrid.numJobs was
reset within the scheduler (Listing 7, line 16),
so that households had to recompute exactly
the same value. Good for the game engine of Prism, but not necessarily for a Monte–Carlo
simulator.
Let us modify the method Microgrid.newInterval(), so that numJobs is
not zeroed in the case of the statistical variant:
numJobs.
Now, a household, after the scheduler's first move, may read the initial value of numJobs,
which is correctly zero, as no jobs had been generated so far. In the subsequent moves of
households, the number of jobs is written to the field by the scheduler. The state space grows, but
households may now just read the value in question, instead of computing it by itself.
Let getPrice() be modified to enable that:
getPrice().
And that's it – the automatons will generated as in the previous version of
Microgrid.java if hc is not supplied with the option
-S, that makes Model.isStatistical() true. On the JVM, in turn, a
simulator–tuned version will be run, unless Model.isStatistical() is made false
by setting a system property hc.statistical=false, e.g. by a JVM's -D option.
As simulators are often used specially to run large models, let the number of households
in the grid be dependent on Model.isStatistical() as well:
Note that the field is not more final. This is because Verics is more strict on final variables
(also the blank ones)
than a standard Java compiler – Verics won't allow, that two values of a final variable
are ever seen. This is why the compiler analyses the code, that computes a final variable's
initial value for possible reads of the same final variable. In order to do that, the compiler recurses
through method calls amongst other. Yet, the compiler analyses exclusively these methods that belong
to the class, to which also belongs a given final variable. Any methods of foreign classes are thus forbidden
in declarations of finals. In our example, NUM_HOUSEHOLDS belongs to Microgrid,
while isStatistical() belongs obviously to Model. In effect, we need to make
the discussed field non–final, or use an intermediate helper variable, if NUM_HOUSEHOLDS
needs to be final, e.g. to be present in the section of constants in the output file.
Note that a non–final NUM_HOUSEHOLDS won't be added to the state vector, as Verics
finds out, that the variable is never written to within the automaton threads, and thus can
be seen by the automatons merely as a constant.
6.5. External constants
Sometimes it is desired to define a constant value not within the model sources, but at the command
line, of either Verics or a model checker.
Let us modify Microgrid.java once again to use external constants.
Let there be two constants, whose values are missing from the model specification:
and
The field Microgrid.NUM_HOUSEHOLDS must be set at Verics' command line, as the
main thread makes use of that field's value:
$ hc Microgrid.java –const HOUSEHOLDS=3~9:2 -op -v0 -sh -i
See that there is a set of values that specifies the number of households: 3 to 9 with
the step of 2.
If there is at least a single constant with multiple values, Verics changes the
structure of the output files into that of an key.txt contains the key to the naming of the
generated files.
The field Household.PRICE_LIMIT does not need to be specified during
hc's work, but it needs to be specified somewhere before the model can
be computed, for example at #Prism!'s command line:
$ prism -const PRICE_LIMIT=1.5 Microgrid/3.nm Microgrid/3.pctl
If the model is run on the JVM, the constants should be defined as system properties
whose names begin with hc.const., e.g.
$ java -Dhc.const.HOUSEHOLDS=3 -Dhc.const.PRICE_LIMIT=1.5
-cp $HC_HOME/lib/hc.jar:. example/Microgrid
7. Bibliography
- H. Hildmann and F. Saffre. Influence of variable supply and load flexibility on demand-side management. In Proc. 8th International Conference on the European Energy Market (EEM’11), pages 63–68, 2011.
- M. Kwiatkowska, G. Norman and D. Parker. PRISM 4.0: Verification of probabilistic real-time systems. In G. Gopalakrishnan and S. Qadeer, editors, Proc. 23rd International Conference on Computer Aided Verification (CAV’11), volume 6806 of LNCS, pages 585–591. Springer, 2011.
- D. Peled. Ten years of partial order reduction. In A. J. Hu and M. Y. Vardi, editors, Computer Aided Verification, volume 1427 of Lecture Notes in Computer Science, pages 17–28. Springer Berlin Heidelberg, 1998.
Files:
- Microgrid.java: source of the model;
- Microgrid.pctl: properties to compute;
- Microgrid.nm: the resulting Prism file.
Command line:
verics Microgrid.java --const HOUSEHOLDS=3~9:2 -op -v0 -sh -iprism Microgrid.nm Microgrid.pctl